Ver Actividad 13


 Actividad 13
Actividad 13

 Actividad 13
Actividad 13
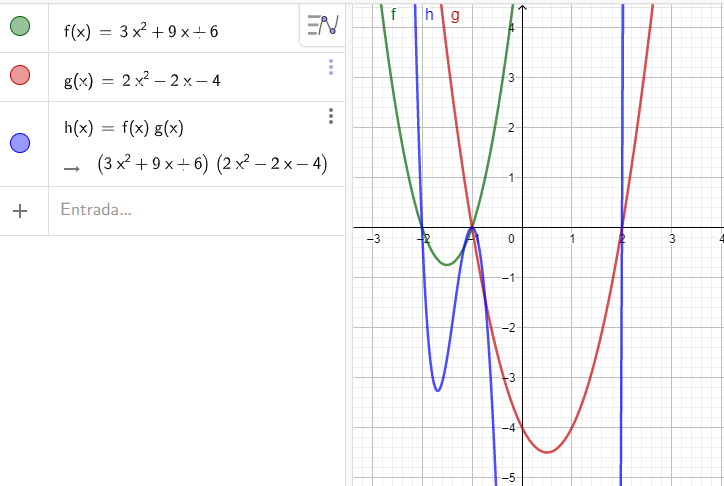
Ingresen en la barra de entrada las fórmulas de f y g de
la actividad 12 y luego \( h(x)=f(x) \cdot g(x) \) (función “producto”).
Las recordamos:
\( f(x)=3x^2+9x+6 \) y
\( g(x)=2x^2-2x-4 \)
Ingresen al
enlace
de GeoGebra
, donde se presentan los gráficos y las fórmulas de las funciones
f, g y h.
Para realizar la actividad, descarguen el archivo correspondiente . Escriban sus respuestas e incluyan capturas de pantalla o fotos de los gráficos estudiados y envíenlos por el buzón que encontrarán más abajo.
La configuración inicial de GeoGebra hace que los gráficos estén fijos, no se pueden mover. En el archivo de la actividad 13 se explica cómo moverlos.
Una vez hecho esto les proponemos responder las siguientes preguntas:
a) ¿Es posible lograr que el polinomio h
tenga cuatro
raíces moviendo la función f? Si es posible dar una fórmula para
h
. Si no es posible, explicar por qué.
b) ¿Es posible lograr que el polinomio h
tenga dos
raíces moviendo la función f? Si es posible dar una fórmula para
h. Si
no es posible, explicar por qué.
c) ¿Es posible lograr que el polinomio h
tenga una raíz moviendo la función
f
? Si es posible dar una fórmula para h
. Si no es posible, explicar por qué.
d) Ingresar nuevamente las funciones f
,
g y
h
originales. ¿Es posible lograr que el polinomio h
tenga una sola raíz permitiéndose mover las dos funciones cuadráticas
f
y g? Si es posible dar una fórmula para
h
. Si no es posible, explicar por qué.
e) ¿Es posible
lograr que el polinomio h
no tenga raíces permitiéndose mover las
dos funciones cuadráticas f y
g? Si es posible dar una fórmula
para h. Si no es posible, explicar por qué.
Volver Atrás
Ingresen en la barra de entrada las fórmulas de f y g de
la actividad 12 y luego \( h(x)=f(x) \cdot g(x) \) (función “producto”).
Las recordamos:
\( f(x)=3x^2+9x+6 \) y
\( g(x)=2x^2-2x-4 \)
Ingresen en la barra de entrada las fórmulas de f y g de la actividad 12 y luego \( h(x)=f(x) \cdot g(x) \) (función “producto”).
Las recordamos:
\( f(x)=3x^2+9x+6 \) y \( g(x)=2x^2-2x-4 \)
Ingresen al
enlace
de GeoGebra
, donde se presentan los gráficos y las fórmulas de las funciones
f, g y h.
Para realizar la actividad, descarguen el archivo correspondiente . Escriban sus respuestas e incluyan capturas de pantalla o fotos de los gráficos estudiados y envíenlos por el buzón que encontrarán más abajo.
La configuración inicial de GeoGebra hace que los gráficos estén fijos, no se pueden mover. En el archivo de la actividad 13 se explica cómo moverlos.
Una vez hecho esto les proponemos responder las siguientes preguntas:
a) ¿Es posible lograr que el polinomio h
tenga cuatro
raíces moviendo la función f? Si es posible dar una fórmula para
h
. Si no es posible, explicar por qué.
b) ¿Es posible lograr que el polinomio h
tenga dos
raíces moviendo la función f? Si es posible dar una fórmula para
h. Si
no es posible, explicar por qué.
c) ¿Es posible lograr que el polinomio h
tenga una raíz moviendo la función
f
? Si es posible dar una fórmula para h
. Si no es posible, explicar por qué.
d) Ingresar nuevamente las funciones f
,
g y
h
originales. ¿Es posible lograr que el polinomio h
tenga una sola raíz permitiéndose mover las dos funciones cuadráticas
f
y g? Si es posible dar una fórmula para
h
. Si no es posible, explicar por qué.
e) ¿Es posible lograr que el polinomio h no tenga raíces permitiéndose mover las dos funciones cuadráticas f y g? Si es posible dar una fórmula para h. Si no es posible, explicar por qué.